Post
viewed 2628 times
-
- 2
සංකීර්ණ සංඛ්යා හා ඒකක වෘත්තය - ක්වොන්ටම් පරිඝණක ක්රමලේකනය සදහා - sa\nkiirNa sa\nkhyaa haa eakaka wruththaya - kwontam parighaNaka kramaleaikanaya sadhahaaසංකීර්ණ සංඛ්යා හා ඒකක වෘත්තය - ක්වොන්ටම් පරිඝණක ක්රමලේකනය සදහා
sa\nkiirNa sa\nkhyaa haa eakaka wruththaya - kwontam parighaNaka kramaleaikanaya sadhahaa සංකීර්ණ සංඛ්යා යනු මනඞකල්පිත කොටසක් සහිත සංඛ්යාය. එම මනහ්කල්පිත කොටස නම් යන්නයි. මෙය i අකුරෙන් දැක්වෙන අතර මෙම නිසා i2 = -1 . එනම් එම සංඛ්යාවෙන්ම වැඩි කිරීමෙන් සෘණ අගයක් ලැබෙන සංඛ්යාවක් මනහ්කල්පිත කල්පිත සංඛ්යාවක් වේ. මෙය සිදුවිය නොහැකි නිසාම මනහ්කල්පිත නමභාවිතා වුවද ගණනය කිරීම් වලදී මෙය ස... sa\nkiirNa sa\nkhyaa yanu manaඞkalpitha kotasak sahitha sa\nkhyaaya. ema manahkalpitha kotasa nam yannayi. meya i akuren dhaekwena athara mema nisaa i2 = -1 . enam ema sa\nkhyaawenma waedi kiriimen sruNa agayak laebena sa\nkhyaawak manahkalpitha kalpitha sa\nkhyaawak weai. meya sidhuwiya nohaeki nisaama manahkalpitha namabhaawithaa wuwadha gaNanaya kiriim waladhii meya sa...සංකීර්ණ සංඛ්යා යනු මනඞකල්පිත කොටසක් සහිත සංඛ්යාය. එම මනහ්කල්පිත කොටස නම්
යන්නයි. මෙය i අකුරෙන් දැක්වෙන අතර මෙම නිසා i2 = -1 . එනම් එම සංඛ්යාවෙන්ම වැඩි කිරීමෙන් සෘණ අගයක් ලැබෙන සංඛ්යාවක් මනහ්කල්පිත කල්පිත සංඛ්යාවක් වේ. මෙය සිදුවිය නොහැකි නිසාම මනහ්කල්පිත නමභාවිතා වුවද ගණනය කිරීම් වලදී මෙය සැබැවින්ම උපකාරීවේ. කිසියම් ගණනය කිරීමකදී අප කටු කොලයක් භාවිතා කර පසුව නියම උත්තරය පොතක ලියන්නාක් මෙන් ගණිත කර්ම වලදී අප යම් යම් ගැටලු මෙම මනහ්කල්පිත අංක සහිත සංකීර්ණ අවකාශය තුල සිදු කර අවසාන උත්තරය නැවතත් නියම සංඛ්යා ලෙස ලබා ගනු ලැබේ. මෙම මනහ්කල්පිත සංඛ්යා වලට ගණිතයේදී අතාත්වික සංඛ්යා යැයි ියනු ලැබේ.
සංකීර්ණ සංඛ්යාවක් යනු a + ib වේ. a යනු ඕනෑම සැබෑ සංඛ්යාවකුයි . සෑම සංකීර්ණ සංඛ්යාවකටම එය හා බැදුනු ප්රතිබද්ධය යන්නක් ඇත. එනම් a + ib සංඛ්යාවේ ප්රතිබද්ධය (a-ib) වේ.
(a+ib) (a-ib) = a2-aib + aib– ib2
i2 = -1 නිසා
= a2 +b2 (මෙමගින් පෙන්නුම් කලේ ප්රතිබද්ධය භාවියෙන් මනඞකල්පිත කොටස ඉවත්ව නැවතත් තාත්වික සංඛ්යාවක්ම ලබා ගැනීමට හැකි බවයි.)
සංකීර්ණ සංඛ්යා තාත්වික කොටස අතාත්වික කොටස 3 + 2i 3 2 5 5 0 −6i 0 −6 සාමාන්ය සංඛ්යා යනුද සංකීර්ණ සංඛ්යා වේ. මන්ද සංකීර්ණ සංඛ්යාවක සංකීර්ණ කොටස i සමග බින්දුව වීමටද (උදා ib = 0) හැකි බැවිනි.

සංකීර්ණ සංඛ්යා අපට ශ්රිතයක් ඇසුරින් මෙසේ නිරූපනය කල හැත මෙම අවකාශය සංකීර්ණ අවකාශය ලෙසද ශ්රිතය ආගන්ඩ් තලය ලෙසද හදුන්වනු ලැබේ. . මෙම ශ්රිතයේ x යනු සැබෑ සංඛ්යාවක් වන විට y යනු අතාත්වික කොටසයි.x2 - 1 = 0 යන ශ්රිතය සැලකුවහොත් අපට බැලූ බැල්මට මෙහි විසදුමක් දැකිය නොහැක. නමුත් විසදුමක් තිබිය යුතු බවද පැහැදිලිය. ආතාත්වික සංඛ්යා පිහිටට එන්නේ මෙවැනි ගැටලු හමුවේයි.
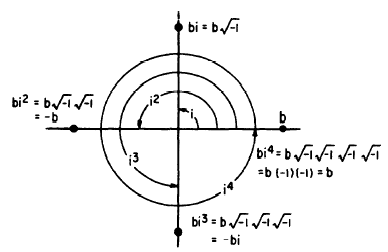
නමුත් ආතාත්වික සංඛ්යා භාවිතයට ගැනීමෙන් අපට x අක්ෂය කැපෙන ලක්ෂ -i හා +i ලෙස වටහා ගත හැක. සරලව විසදුම ඇත්තේ අපට පෙනෙන මානයේ නොව සංකීර්ණ අවකාශය තුලයි.අතාත්වික සංඛ්යාවක් එම ආතාත්වික සංඛ්යාවෙන්ම ගුණ කරනවා යනු එම ගුණ කරන වාරයක් පාසා එය ,
,-1,1 ලෙස එකම ලක්ෂය ඔස්සේ කරකැවේ.
= -1 , -1
=
,
=1
අතාත්වික සංඛ්යාව සංඛ්යා ඉංග්රීසි i අකුරෙන් නිරූපනය කෙරේ.
එවිට සංකීර්ණ සංඛ්යාවක් යනු a + ib වේ. a යනු ඕනෑම සැබෑ සංඛ්යාවකුයි . සෑම සංකීර්ණ සංඛ්යාවකටම එය හා බැදුනු ප්රතිබද්ධයක් ඇත.. එනම් a + ib සංඛ්යාවේ ප්රතිබද්ධය(a-ib) වේ.
(a+ib) (a-ib) = a2-aib + aib– ib2
i2 = -1 නිසා
= a2 +b2 (මෙමගින් පෙන්නුම් කලේ ප්රරතිබද්ධය භාවියෙන් අතාත්වික කොටස ඉවත්ව නැවතත් සැබෑ සංඛ්යාවක්ම ලබා ගැනීමට හැකි බවයි.)
සාමාන්ය සංඛ්යා යනුද සංකීර්ණ සංඛ්යා වේ. මන්ද සංකීර්ණ සංඛ්යාවක ඕනෑම අගයක් බින්දුව වීමටද (උදා b = 0) හැකි බැවිනි.
අවස්ථාවේදී |A> යනු සංකීර්ණ සංඛ්යා පෙලක් නම් |>|a>
a+bi ආදී සංකීර්ණ සංඛ්යා 2x2 න්යාස ලෙසද දැක්විය හැක.
සාධනය මෙතනින්ඔයිලර් ගේ සමීකරණය
ක්වොන්ටම් යාන්ත්ර විද්යාවේදී ගණනය කිරීම් වලදී ඉතාමත්ම වැදගත් වන සම්බන්ධයක් ඔයිලර් ගේ සමීකරණය ලෙස හැදින් වේ.සංකීර්ණ සංඛ්යාවන් වුනු මෙය
=
ලෙස දක්වනු ලැබේ.
ඡායාරූප උපුටා ගෙන ඇති නිසා පහත රටාවේ, x මගින් දක්වා ඇත.
ඕනෑම cos x හෝ sin x සදහා
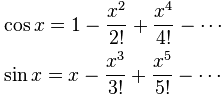
(! යනු ඖනෑම සංඛ්යාවක් සදහා 3! = 1 x 2 x 3, 4! = 1 x2 x 3 x 4 වේ)
සත්ය වේ .
පහත රටාව සලකන්න.
x සදහා කුමන අගයක් යෙදුවද රටාවේ එකතුව 2.718281828459045 ට ආසන්න වේ.
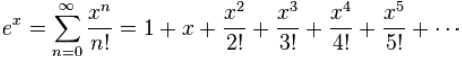
මෙම රාශියට i එකතු කිරීමෙන්
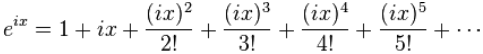
i අගයන් වර්ගය අනුව සුලු කිරීමෙන් ()
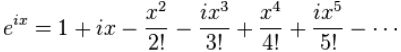
i අගයන් සහිත කොටස් වෙන් කර i පිටතට ගැනීමෙන්
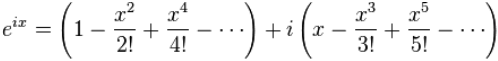
මෙය ඉහත cos හා sin සදහා ලැබුනු කොටස්ම බව පැහැදිලි වනු ඇත .
එම නිසා. x ,මගින් නිරූපනය වේ.
අපට ඛන්ඩාංක තලයක (සංකීර්ණ ඛන්ඩාංක තලයක) නිරූපනය කල හැක.
කුමණ අගයක් ගත්තද මෙය සෑම විටම අපට අරය 1 වූ වෘත්තයක් මත පිහිටි කෝණයක් ගෙන දේ. මෙය ඒකක වෘත්තය නැතිනම් unit circle ලෙස හැදින්වේ.
, රේඩියන් හෝ ඕනෑම අගයක් සදහා මෙය වලංගුය. මෙම ඒකක වෘත්තය වැදගත් වන්නේ ගණනය කිරීම් මේ හරහා සුලු කර ගැනීම හැකි වීමයි. උදාහරණයක් ලෙස තරංගයක කම්පනය අපට මෙම වෘත්තයේ මධ්යා ලක්ෂය වටා භ්රමණය වන වාරගණනින් නිරූපනය කල හැක. අරය1 බැවින් sin සහ cos ආදී ත්රිකෝණ මිතික ගණනය කිරීම්ද පහසු වේ. එසේම මෙය ත්රිමාණ ගෝලයක් ලෙස සැලකීමෙන් ක්වොන්ටම් බිටු නිරූපනය කිරීම සදහා ත්රිමාණ අවකාශයේ ඉලෙක්ට්රෝණයක භ්රමණය නිරූපනය එය තුලින් සිදු කෙරේ. මෙම ගෝලය බ්ලොච් ස්පියර් ලෙස හැදින් වේ.
+1 = 0 යන්න ද මෙවැනිමය.
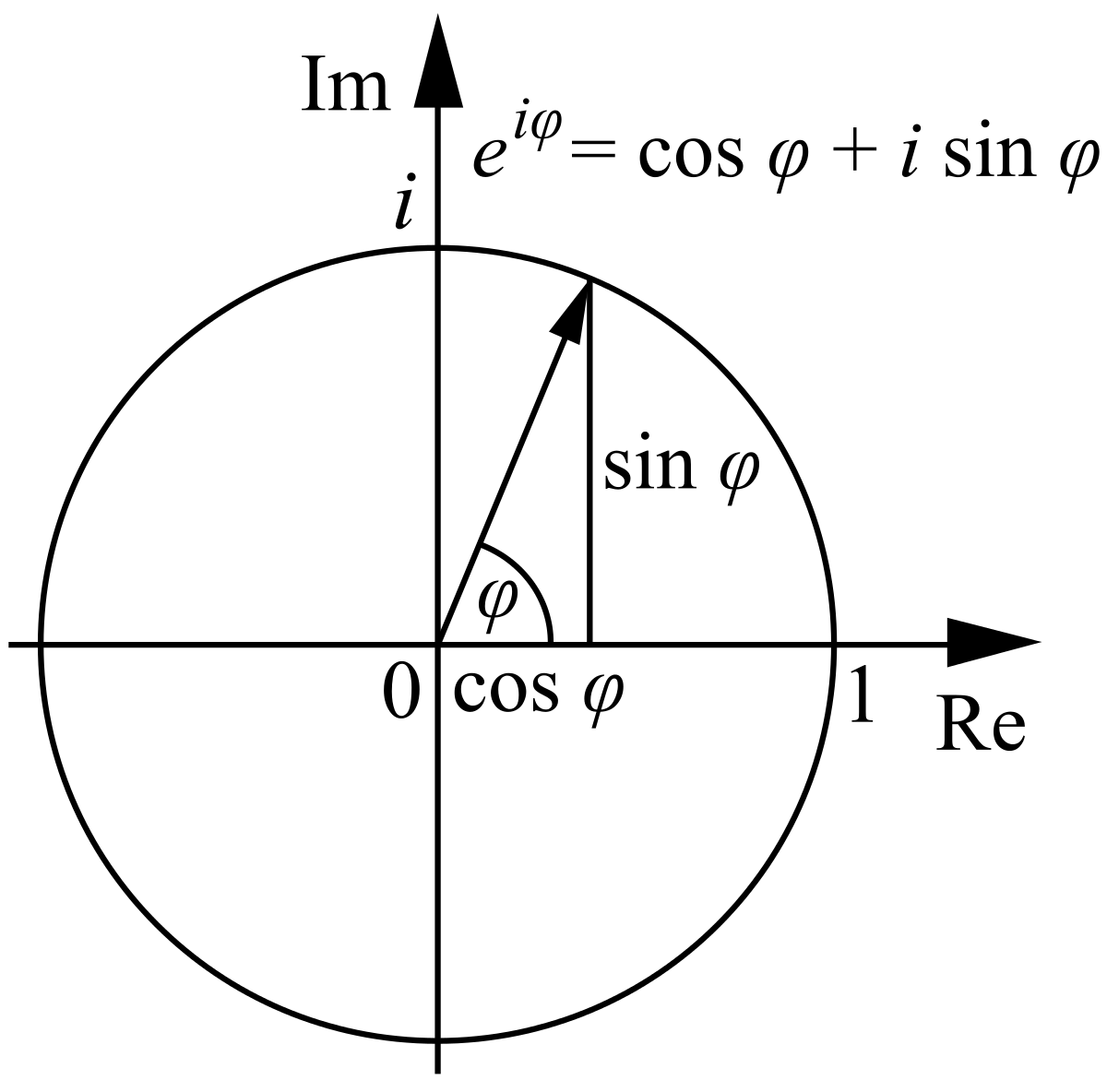
පහසුවෙන් ත්රිකෝණමිතිය මතක් කර ගැනීමට පහත රූපය උදව් කරගන්න.


